Modèles
de pneu sous charge latérale
Les modèles employés pour
représenter le comportement d'un pneu ne sont pas phénoménologiques, dans la
mesure où ils ne sont pas dérivés des propriétés du matériau ou de la structure du pneu. Dans le modèle le
plus communément employé, on décompose la zone de
contact en éléments indépendants, chacun étant relié au sol par une raideur
latérale. Un autre modèle, celui de la
corde, introduit la notion de tension
entre des éléments successifs. Enfin, un modèle de
poutre introduit la flexion entre un élément et ses voisins. Revenons au
premier :
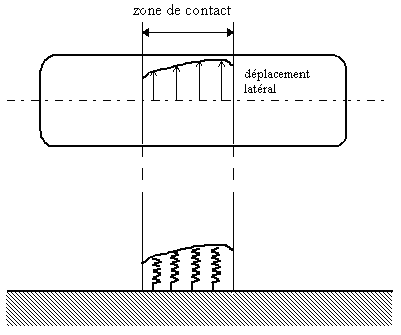
Le déplacement de la bande de
roulement peut être représenté comme suit :
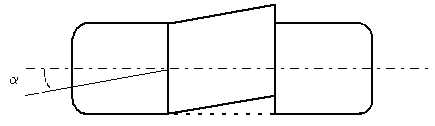
Cette modélisation permet
de calculer la force nécessaire pour
écarter un élément de longueur dx d'une
longueur d :
dF = c.d.dx.
En intégrant sur la
longueur L de la zone de contact, on a donc
F = Int0->L
[c.d]dx
Le moment exercé autour de l'axe vertical est
M = Int0->L [c.d (x-L/2)]dx
La force normale par
unité de longueur étant supposée
uniforme, donc égale à Fv/L, la condition de non-glissement s'écrit
c.d < \mu.Fv/L
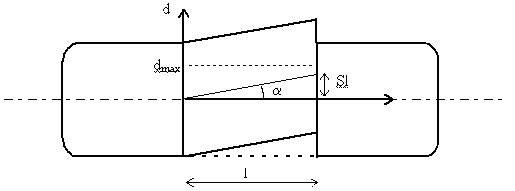
Le déplacement latéral
maximum est donc
dmax = \mu.Fv/(L.c)
Si l'on note S =
tan(\alpha) le glissement latéral, on a pour des petits angles de glissement
d = L.tan(\alpha) = S.L,
donc S < dmax
/ L, soit
S < \mu.Fv /
(L2.c)
En prenant les valeurs
suivantes :
longueur
de la zone de contact : 180 mm
force verticale = 5 kN
coefficient de frottement = 1.0
raideur c = 3 MPa,
on obtient un angle de
glissement de l'ordre de 3o, et un déplacement
correspondant de 9 mm. Pour des
glissements aussi limités, l'hypothèse faite que le déplacement est
"triangulaire" est à peu près valable. La force latérale est alors
proportionnelle au glissement :
Fy = ½ cL2S
soit, comme S ~ \alpha
pour des petits glissements,
Fy = ½ cL2 \alpha
La raideur associée ky
= dFy/d\alpha est donc ½ cL2 (soit de l'ordre de
50 kN/rad avec les valeurs numériques retenues ci-dessus). La force maximum de non-glissement est ½ cdmaxL,
soit ½ \mu Fv. Un tel modèle prédit donc que le glissement
intervient lorsque la force latérale atteint la moitié de la force de
frottement totale "disponible".
La résultante de la force latérale agit
au centre de gravité du triangle, donc
à L/6 en arrière du point milieu (c'est ce qu'on appelle la chasse pneumatique). Le moment
d'auto-alignement est alors
Mz = Fy L/ 6 = cL3S / 12
ce qui est donc
proportionnel au glissement. La chasse
pneumatique mesurée en pratique est plus importante (t/L étant de l'ordre de
0.2 à 0.35) pour des petits angles de
glissement.
Il est important de noter que la pente de la courbe entre force latérale et glissement ne dépend pas
du coefficient de frottement au sol,
mais de la raideur c, donc de celle due à la carcasse et à la bande de roulement.
Lorsque l'angle de
glissement augmente encore, on passe dans la situation suivante :
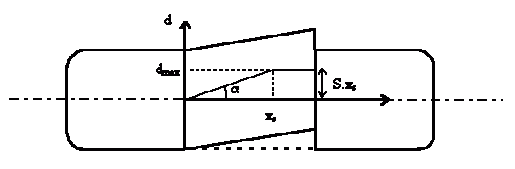
La zone xs
< x < L est appelée zone de
glissement. On a S = dmax / xs, soit, compte tenu de :
dmax = \mu Fv / (cL),
xs = \mu Fv /
(cLS)
Le calcul de la force latérale donne alors
Fy = \mu Fv -
(\mu2Fv2)/(2cL2S)
Le moment
d'auto-alignement est après calcul
Mz = (cLdmax2)/(4S) - (cdmax3)/(6S2)
On constate donc que pour
un angle plus grand que la limite de non-glissement, le moment
d'auto-alignement peut diminuer même si la force augmente.
Ce modèle, bien que fort
simple, permet donc de dériver des
courbes en bon accord avec les données expérimentales, à condition de calibrer les paramètres empiriques. La
principale différence vient de ce que
l'on observe expérimentalement des moments d'auto-alignement négatifs pour de grands angles de glissement. Ceci est dû entre autres à la dissymétrie
avant/arrière de la distribution de la force verticale, qui permet un
frottement plus important dans la moitié avant de
la zone de contact.
La raideur transversale ky
introduite ci-dessus est en général normalisée par la force verticale Fv
pour donner ce qu'on appelle le coefficient de
raideur transversale Cs :
Cs = ky / Fv
Cs est de l'ordre de
10/rad pour un pneu radial, et de 8/rad
pour un pneu diagonal.
On peut revenir au repère
véhicule pour décomposer la force latérale en ses composantes centrale et de traînée. Comme l'accélération centripète
est donnée par la force centrale, cela permet de
constater qu'elle passe par un maximum pour un angle
d'environ 20o, pour diminuer ensuite.
Le ratio (force de traînée)/(force centrale) est similaire au
ratio traînée/portance pour une aile. En négligeant la résistance au roulement,
il se réduit au glissement. On comprend donc l'intérêt de pneus à grande raideur latérale, puisque la traînée est
moindre pour un même effort central.