Efforts latéraux 

Sans contraintes, une roue est en équilibre vertical, et roule suivant son plan de symétrie. Dès lors que la direction de déplacement n'est plus dans ce plan de symétrie, une force latérale se développe. Une composante importante de cette force est la force de glissement, associée à ce qu'on appelle l'angle de glissement, c'est-à-dire l'angle, noté \alpha, entre l'axe longitudinal de la roue et la direction de déplacement :

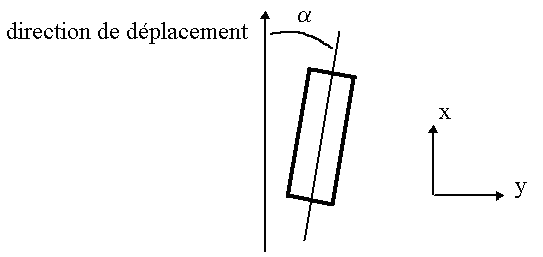
La force latérale dépend également, mais dans une moindre mesure, de l'angle de carrossage entre le plan de la roue et la verticale, noté \gamma. La composante associée est nommée force, ou poussée, de carrossage :

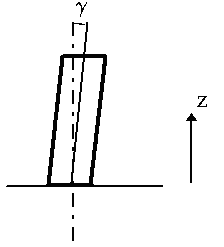
Cette force de carrossage est approximativement proportionnelle à l'angle de carrossage, ce qui permet de définir la raideur de carrossage k_c, de l'ordre de 2kN/rad pour un pneu radial de voiture. Elle est également proportionnelle à la force verticale, ce qui nous amène à définir un coefficient de raideur de carrossage c_c.

On a donc, lorsque le glissement est nul :

F_y = k_c \gamma = c_c F_v \gamma

c_c vaut à peu près 1.0 pour un pneu diagonal, et 0.4 pour un pneu radial. Même si les angles de carrossage sont réduits (inférieurs à 1^o en statique, pas plus de 10^o dans les conditions extrêmes), les forces développées peuvent avoir des conséquences non négligeables sur la tenue de route des véhicules, principalement à cause de la variation de carrossage lors des mouvements de suspension, qui peuvent être différents entre les trains avant et arrière.

La poussée de carrossage se superpose de manière algébrique à l'effort latéral, et peut permettre d'augmenter la valeur de crête de celui-ci si le carrossage est "du bon côté". En pratique, on ne peut évidemment pas augmenter le carrossage indéfiniment, pour des raisons d'uniformisation de l'échauffement et de l'usure de la bande de roulement. Pour des pneus larges de route, l'effort de carrossage tend à s'effondrer au-delà de 5°. Pour les pneus à section circulaire utilisés sur les motos, l'effort de carrossage reste important jusqu'à près de 50°.

On considère généralement que les effets de glissement et de carrossage sont indépendants, et donc que l'on peut décomposer la force latérale de manière unique :

F_y = F_g + F_c
     = k_g \alpha + k_c \gamma
     = F_v (c_g \alpha + c_c \gamma)

Ceci n'est plus tout à fait vrai en régime non-linéaire, c'est-à-dire pour des angles importants. Sur une moto, par exemple, la raideur latérale diminue considérablement avec l'angle de carrossage lorsque celui-ci atteint des valeurs élevées. La diminution de c_g est de l'ordre de 0.3 à 0.7 % par degré d'angle de carrossage, relation pratiquement linéaire jusqu'à 60^o de carrossage.