Dynamique du véhicule en régime permanent

Nota : on appelle "gain" la sensibilité de la réponse d'une quantité quelconque à l'angle de braquage.

La courbe de base en dynamique du véhicule est celle qui donne l'angle de braquage en fonction de l'accélération latérale pour un rayon de trajectoire donné. L'angle de braquage est la somme de l'angle de braquage cinématique a_cin déjà vu, et d'un terme appelé angle de braquage dynamique, qui est l'angle supplémentaire requis pour obtenir l'accélération latérale voulue.

Il y a deux approches principales pour représenter la dynamique du véhicule en régime permanent. La première est la méthode dite cinématique, car elle relie des termes cinématiques (rayon de courbure, vitesse de lacet, accélération latérale) aux grandeurs d'entrée (vitesse et braquage au volant). La seconde, plus complexe, est la méthode des moments, et étudie la force latérale et le moment de lacet en fonction du lacet et du braquage. Cette méthode sera davantage utilisée dans le domaine transitoire, et on se limitera ici principalement à la première.

Le modèle le plus simple pour cette étude est celui dit "2 roues". On réduit en fait la paire de roues d'un essieu à une seule roue, et on néglige toute suspension. Ce modèle n'a qu'un lointain rapport avec celui d'une moto, car on ne tient pas compte ici de la capacité des deux-roues à se pencher dans les virages.

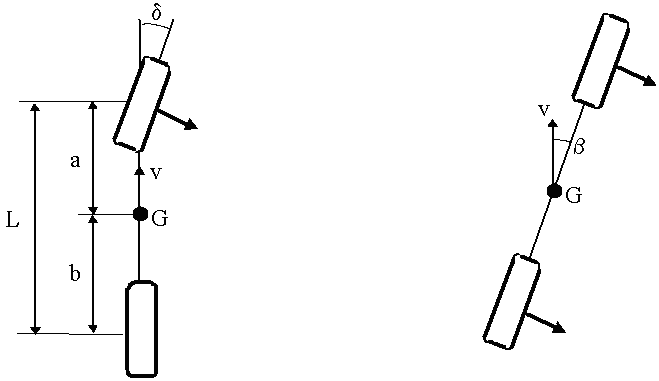
Une accélération latérale donnée a_lat impose un même facteur F_y/m à l'avant et à l'arrière. A ce facteur correspondent deux angles de glissement \alpha_av et \alpha_ar (il n'y a aucune raison pour que ces angles soient identiques ...). Le conducteur doit donc fournir un "complément" de braquage égal à la différence entre ces angles de glissement. On appelle ainsi angle de sous-virage \alpha_sv la différence \alpha_av - \alpha_ar. C'est l'angle de braquage dynamique dont on parlait ci-dessus.

On a vu plus tôt qu'en cas d'accélération latérale réduite, l'angle de braquage cinématique est approché par L/R. On peut donc écrire, dans le cas général, que l'angle de braquage est

\delta = L/R + \alpha_sv

On peut réécrire cette expression sous la forme R = L / (\delta - \alpha_sv)

On constate alors que lorsque \alpha_sv augmente, le rayon augmente.

Typiquement, les essais de caractérisation d'un véhicule passent par un test standard, qui consiste à faire évoluer le véhicule sur un virage à rayon constant, et à augmenter progressivement la vitesse. Une caractéristique importante de sa dynamique est donnée par l'allure de la relation entre l'angle de braquage à imprimer au volant pour maintenir le rayon de courbure fixé et l'accélération latérale. Cette courbe est à peu près linéaire jusqu'à 3 m.s^-2, voire 4.5 m.s^-2 pour une voiture performante. On appelle ça le régime dynamique primaire. Le régime secondaire va de 3 à 6 m.s^-2, les transferts de charge latéraux devenant importants. Au-delà, les effets de friction sont prépondérants ...

Dans le domaine primaire, on peut écrire

\delta = L/R + k_sv a_lat

où k_sv est le gradient (ou coefficient) de sousvirage et a_lat l'accélération latérale. Une valeur typique pour k_sv est 3 deg/g.

Plus formellement, k_sv est défini par d\alpha_sv/da_lat.

Si R n'est pas constant, la composante cinématique de l'angle de braquage varie aussi et vaut a_cin = L/R = La_lat/v². On appelle gradient d'angle de braquage cinématique le coefficient

k_cin = da_cin/da_lat = L/v².

Si l'on note \rho = 1/R la courbure, on a :

\delta = \rho (L + k_svv²)

Le gain de la réponse en courbure G = d\rho / d\delta s'écrit alors

G = (1/(1+(k_sv/L)v²))/L

Il dépend donc du carré de la vitesse, et cette dépendance est influencée par le rapport k_sv/L, parfois appelé facteur de stabilité f_s. On définit, en faisant l'hypothèse que k_sv est positif, une vitesse caractéristique v_ca = (L/k_sv)^1/2. Dans le cas d'un véhicule survireur, donc d'un k_sv négatif, on parlera plutôt de vitesse critique v_cr = (-L/k_sv)^1/2.

On désigne par facteur de réponse f_r la part du terme de vitesse dans l'expression de G :

f_r = (1/(1+(k_sv/L)v²))

et son inverse U = 1/f_r est le facteur de sousvirage : U = 1+(v/v_ca)²

Un facteur de réponse élevé signifie que pour une consigne donnée au volant la réponse latérale sera importante. Si k_sv est positif, le facteur de réponse diminue avec la vitesse. Si k_sv est négatif, en revanche, le facteur de réponse tend vers l'infini lorsque la vitesse tend vers la vitesse critique : un tel véhicule est directionnellement instable.

Sous-virage et sur-virage

"Le sous-virage, c'est quand le conducteur a peur. Le sur-virage, c'est quand le passager a peur" (Anon.)

Si cette expression laisse entendre ce que signifient sous- ou sur-virage dans des conditions limites, il faut précisément faire la distinction entre ces conditions limites et des conditions plus "normales". Les notions associées n'ont alors pas forcément exactement la même signification.

Il faut tout d'abord bien comprendre que le sous-virage est donné par le signe du gradient de sous-virage k_sv = (d\delta / da_lat)R, et non par le simple angle de sous-virage. On peut très bien avoir un angle de sous-virage positif et en même temps un gradient négatif.

La représentation du comportement d'un véhicule en régime primaire et permanent peut être ramenée à trois quantités constantes : le gradient de roulis k_rou, le gradient d'attitude k_att, et le gradient de sous-virage k_sv. Les deux premiers sont les coefficients de proportionnalité reliant les angles de roulis et d'attitude à l'accélération latérale. On a donc, en régime linéaire :

\phi = k_rou a_lat

puisqu'on peut faire l'hypothèse que le roulis est nul lorsque l'accélération latérale l'est également, et

\beta = k_att a_lat + \beta_cin

où \beta_cin est l'angle d'attitude cinématique -b/R

k_rou dépend de la hauteur du barycentre des masses suspendues, de la raideur totale en roulis et de la hauteur de l'axe de roulis. k_att dépend principalement du coefficient de raideur transversale des pneus arrière.

Revenons au modèle à deux-roues déjà vu, et intégrons l'effet de la suspension. On écrit alors

\delta = L/R + (a_gAV - a_gAR) + \delta^susp_AV + \delta^susp_AR

où \delta^susp_AV et \delta^susp_AR sont notés positifs lorsqu'ils vont dans le sens du sous-virage. Ainsi, \delta^susp_AV est positif lorsque la roue avant essaie de diminuer l'effort latéral, et \delta^susp_AV est positif lorsque la roue arrière essaie d'augmenter cette force latérale.

Le gradient correspondant de l'angle de braquage est

k_br = k_cin + k_susp + k_pn

où k_susp est la somme des termes dus à la géométrie et aux flexibilités et k_pn est le gradient dû au pneu d\alpha_sv\da_lat. L'effet géométrique provient du braquage et du carrossage induits par le roulis.

La tableau ci-dessous résume les contributions (en degrés par g) des différents éléments pour un véhicule standard à différentiel libre :

Facteur	Avant	Arrière	Avant - Arrière
Flexibilité du pneu	6	6	0
position du centre de masse	0.6	-0.6	1.2
variation	-0.3	0.3	-0.6
braquage induit par le roulis	0.5	-0.5	1.0
effet sur le braquage du carrossage induit par le roulis	0.2	0.5	-0.3
flexibilité due à l'effort latéral	0.2	0.2	0
flexibilité due au moment d'alignement	1.1	0.1	1.0
Total	8.4	5.9

La différence des deux colonnes (ici 2.5) donne le gradient de sous-virage.

Etudions maintenant plus en détail les contributions à k_att et k_sv. Sur un modèle à deux roues de raideur latérale k_lat identique à l'AV et à l'AR, et dont le centre de gravité est à mi-empattement, on a

\alpha_AV = \alpha_AR = ma_lat/(4k_lat)

soit

k_att = m/(4k_lat) et k_sv = 0.

Avec m =1200 kg et k_lat = 500 N/deg, les ordres de grandeur sont donc k_att = 6 deg/g.

Si, maintenant, G est en avant du point milieu, on arrive à 

\alpha_AV = bma_lat/(Lk_lat)
\alpha_AR = ama_lat/(Lk_lat)

soit

k_att = am/(Lk_lat)
k_sv = m(b-a)/ (2Lk_lat)

Les ordres de grandeur sont maintenant resp. de 5.4 deg/g et 1.2 deg/g. Le fait d'avancer G a donc diminué k_att et augmenté k_sv.